等腰三角形互动答题
通过互动练习掌握等腰三角形知识,提升解题能力
循序渐进
从基础到高级,逐步提升
详细解析
每道题都有详细解答
成就系统
完成挑战获得成就感
轻松入门
逐步进阶
1 已知等腰三角形的两边长分别为4cm、8cm,则该等腰三角形的周长是( )
答案与解析
正确答案:D. 20cm
解:当腰长为4cm时,4+4=8cm,不符合三角形三边关系,故舍去;
当腰长为8cm时,符合三边关系,其周长为8+8+4=20cm.
故该三角形的周长为20cm.
2 已知等腰三角形的一个底角为50°,则它的顶角为( )
答案与解析
正确答案:C. 80°
解:当底角是50°时,
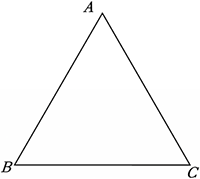
∵ AB=AC,
∴ ∠B=∠C=50°,
∵ ∠A+∠B+∠C=180°,
∴ ∠A=180°-50°-50°=80°.
3 已知等腰三角形的一内角度数为50°,则它的顶角的度数为( )
答案与解析
正确答案:D. 50°或80°
解:如图所示,△ABC中,AB=AC.
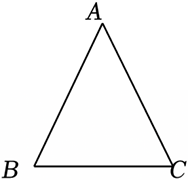
有两种情况:①顶角∠A=50°;
②当底角是50°时,
∵ AB=AC,
∴ ∠B=∠C=50°,
∴ ∠A=180°-50°-50°=80°,
∴ 这个等腰三角形的顶角为50°或80°.
挑战高手
1 在中国古代建筑中,有一种常见的装饰元素叫做"斗拱"。斗拱由多个小木块组成,它们之间通过榫卯结构相互连接,形成了一种独特的美感。如图1,从正面观察斗拱可发现其外轮廓形状类似于一个等腰三角形。如图2,若△ABC的周长为24,一边长为6,则此等腰三角形的底边长是( )

答案与解析
正确答案:A. 6
解:如果等腰三角形的腰长是6,
∴ 等腰三角形的底边长=24-6×2=12,
∵ 6+6=12,不满足三角形三边关系定理,
∴ 等腰三角形的腰长不能是6;
如果等腰三角形的底边长是6,
∴ 等腰三角形的腰长=1/2×(24-6)=9,
∵ 6+9>9,满足三角形三边关系,
∴ 等腰三角形的底边长是6.
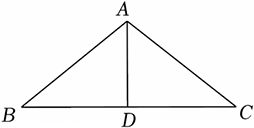
2 如图,在等腰△ABC中,AD⊥BC,∠BAC=110°,∠BAD的度数是( )
答案与解析
正确答案:D. 55°
解:根据等腰三角形三线合一的性质可知:AD⊥BC,∠BAC=110°,
∴ ∠BAD=1/2∠BAC=55°.
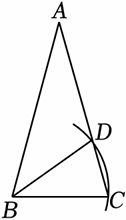
3 如图,在△ABC中,AB=AC,∠A=30°,以点B为圆心,BC的长为半径画弧,交AC于点D,连接BD,则∠ABD=( )
答案与解析
正确答案:B. 45°
解:∵ AB=AC,∠A=30°,
∴ ∠ABC=∠ACB=1/2(180°-∠A)=1/2(180°-30°)=75°,
∵ 以B为圆心,BC的长为半径圆弧,交AC于点D,
∴ BC=BD,
∴ ∠CBD=180°-2∠ACB=180°-2×75°=30°,
∴ ∠ABD=∠ABC-∠CBD=75°-30°=45°.